Camp David, named after its owner David Franklin, was conceived as a civil defense facility for the Town of Bolinas. The Camp David antenna is a dual log-periodic Alexanderson network for high frequency radio communications. Hence forth it will be called the “Bolinas Antenna”. The Bolinas Antenna suited the needs of both Bolinas radio stations KPH and NMC. The “group” did not like this idea so the Bolinas antenna is no more. But the principles are not gone, they exist as mathematical certainties and established engineering formula. The Bolinas antenna is constructed upon two primary engineering considerations: The first is the use of counter-spatial, or reactive, elements, as found in the distributed networks of Tesla and the lumped networks of Alexanderson. The second is the use of a log-periodic sequence of elements as developed thru U.S. Air Force research contracts. The union of these two conditions give rise to a broad bandwidth structure along with “Non Maxwellian” transmission capability. Niether Tesla nor Alexanderson produced such a network, both were very much Single Frequency structures.
The primary objective in the development of the Bolinas Antenna was for telluric transmission and reception in the range of 80 to 40 meters, a one octave band. The Bolinas Antenna consisted of a pair of vertical networks in phase conjunction. The neutral connected directly into the San Andreas Fault line. The log-periodic construction allowed the Bolinas Antenna to also be utilized as an electro-magnetic radiator up to 30 megacycles per second. The compact size and the broadband characteristics make this antenna useful for confined shipboard installations. The theory and design as well as construction details will be developed here.
(II) The counter-spatial, or reactive, transmission network theory is already given in “System for the Transmission and reception of Telluric Electric Waves” by E.P. Dollard. This aspect will therefore not be repeated here. The log-periodic concept will however be developed in the following: Considerable detail on the log-periodic antenna can be found in “The Multi-Wave Oscillator Handbook”, by Tom Brown. A U.S. Psychotronics Assn. Video on the M.W.O. Also exists on “YouTube”. Here can be found the details of my U.H.F. M.W.O. Antenna. Its range was from 300 Mc/sec to 1000 Mc/sec. A “faster than light” speed was expected, but as usual it was time for the “rat to run” so the antenna project vanished to the winds. Be we can rest assured that someone profited from it.
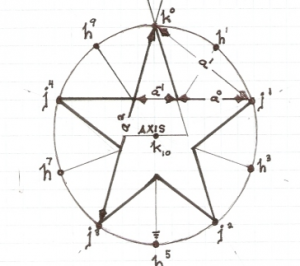
The log-periodic antenna grew out of U.S. AirForce research contracts with the objective of developing a “frequency independent” antenna. The tactical H.F. Radio, and the U.H.F. Spread spectrum systems under development could not operate without such an antenna structure. Unexpectedly here electricity meets with Fibonacci. The log-periodic antennae were found to project themselves into a virtual antenna beyond the physical bounds of their apex. This is analogous to the “plant-archetype” of Rudolf Steiner.
Log-periodic theory states that an electrical structure becomes frequency independent when its constituent sub-structures each exist in a log-periodic sequence. This is to say each elemental network in a series of networks differs from its neighbor networks in a constant logarithmic proportion. Then the concatenated series of networks becomes frequency independent over a finite band, this depending on the total number of individual networks in the log-periodic progression, the more networks the greater the bandwidth.
This log-periodic geometry can be seen in a given rank of organ pipes. The musical scale is a log-periodic sequence in itself. The generalized log-periodic form is derived from the following mathematical expressions:

